Примеры расчетов и практическое применение
Теперь рассмотрим несколько примеров, чтобы лучше понять, как осуществляется расчет модуля перемещения при повороте автомобиля на четверть круга:
Пример 1:
Допустим, у нас есть автомобиль, который поворачивает на четверть круга с радиусом 5 метров. Чтобы рассчитать модуль перемещения, необходимо умножить длину дуги окружности на отношение угла поворота к 360 градусам. В данном случае, длина дуги окружности будет равна (1/4) * 2 * π * 5 = 2,5 * π. Угол поворота составляет 90 градусов. Подставив значения в формулу, получаем: |S| = (2,5 * π) * (90 / 360) = (2,5 * π) * (1/4) = (5/4) * π ≈ 3,93 метра.
Пример 2:
Рассмотрим случай с автомобилем, который поворачивает на четверть круга с радиусом 10 метров. В этом примере, длина дуги окружности будет равна (1/4) * 2 * π * 10 = 5 * π. Угол поворота также составляет 90 градусов. Подставив значения в формулу, получаем: |S| = (5 * π) * (90 / 360) = (5 * π) * (1/4) = (5/4) * π ≈ 7,85 метра.
Практическое применение:
Расчет модуля перемещения при повороте автомобиля на четверть круга имеет практическое применение в различных ситуациях, связанных с автомобильной инженерией и навигацией. Например, это может быть полезно для определения пройденного расстояния при маневрировании на узких улицах или при проектировании автоматических систем управления автомобилем. Такой расчет также может быть использован для определения расстояния, которое автомобиль может пройти за определенное количество поворотов.
Важно помнить, что такой расчет представляет собой упрощенную модель и не учитывает другие факторы, такие как трение и изменение скорости автомобиля. При использовании в реальных условиях, необходимо учитывать эти факторы для получения более точных результатов
Описание модуля перемещения
Двигатель является источником энергии, который преобразует химическую энергию топлива в механическую работу колёс. Он работает на принципе внутреннего сгорания, в результате чего генерируется мощность, необходимая для передвижения автомобиля.
Трансмиссия — это система передачи мощности от двигателя к колёсам. Она получает моторную энергию и передаёт её в правильной пропорции к дифференциалу, который распределяет мощность между колесами.
Подвеска предназначена для амортизации ударов и вибраций, возникающих во время движения. Она обеспечивает баланс и комфортность автомобиля, позволяя колесам подстраиваться под неровности дороги.
Рулевое управление — это система, позволяющая водителю изменять направление движения автомобиля. Она состоит из рулевого механизма, рулевого колеса и связанных с ними компонентов.
Вместе эти компоненты модуля перемещения обеспечивают автомобилю способность к маневрированию, поворотам и движению вперед. Они взаимодействуют между собой, чтобы обеспечить максимальную эффективность и безопасность на дороге.
Практические советы по вычислению модуля перемещения
Вычисление модуля перемещения автомобиля при повороте на четверть круга может быть полезным не только для водителей, но и для всех, кто интересуется движением транспорта и геометрией. Для его вычисления можно использовать следующие практические советы:
1. Измерьте радиус поворота автомобиля. Для вычисления модуля перемещения необходимо знать радиус поворота, который можно получить, измерив длину дуги, по которой автомобиль пройдет во время поворота. Эту длину можно измерить, например, с помощью широкой ленты или использовать формулу для вычисления длины окружности.
2. Узнайте угол поворота автомобиля. Чтобы вычислить модуль перемещения, вам понадобится знание угла поворота автомобиля. Угол можно измерить с помощью специального угломера или использовать градусомер, который есть в большинстве навигационных устройств.
3. Примените известные формулы для вычисления модуля перемещения. После того, как вы определили радиус и угол поворота, можно использовать следующую формулу для вычисления модуля перемещения: Модуль перемещения = 2 * π * радиус * (угол / 360).
4. Используйте таблицу для удобного вычисления. В таблице ниже приведены значения модуля перемещения для различных радиусов поворота и углов поворота:
| Радиус поворота (м) | Угол поворота (градусы) | Модуль перемещения (м) |
|---|---|---|
| 10 | 90 | 15,71 |
| 15 | 180 | 47,12 |
| 20 | 270 | 94,24 |
| 25 | 360 | 157,08 |
Таблица поможет вам быстро определить модуль перемещения для заданного радиуса поворота и угла поворота.
Используя эти практические советы, вы сможете легко вычислить модуль перемещения автомобиля при повороте на четверть круга и применить эту информацию с пользой для решения различных задач.
Задача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
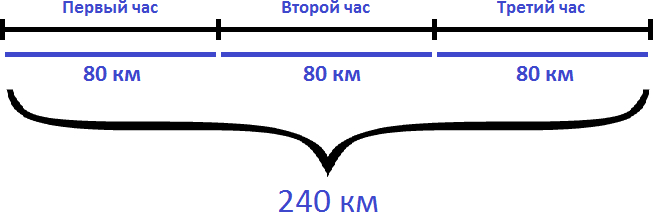
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
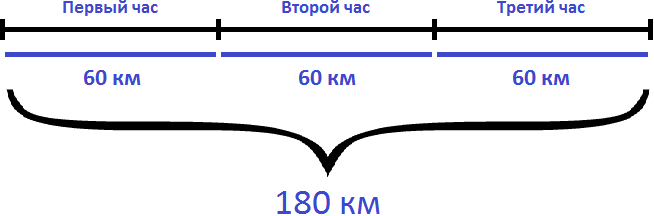
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
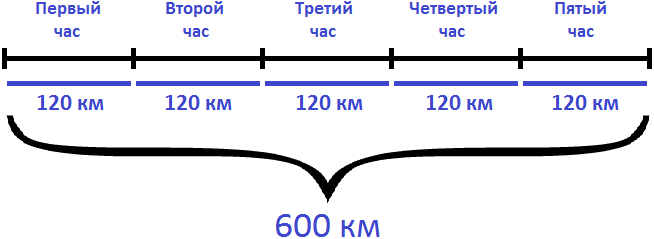
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
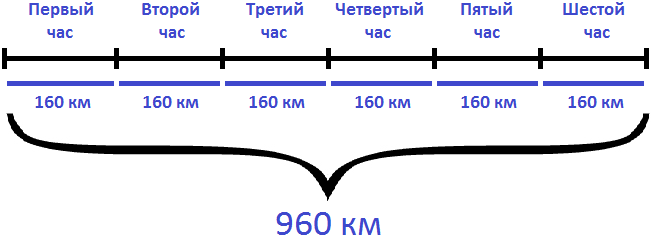
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Измерение угла поворота
Для расчета модуля перемещения при повороте автомобиля на четверть круга необходимо знать угол поворота. Измерение угла поворота может быть осуществлено различными способами. В данной статье рассмотрим два основных способа: с помощью специализированного оборудования и с помощью математических формул.
Первый способ заключается в использовании специализированных датчиков, которые устанавливаются на автомобиль. Эти датчики могут быть различными: гироскопами, акселерометрами, магнитными датчиками и т.д. С их помощью можно получить точные данные об угле поворота автомобиля.
Второй способ базируется на математических формулах и основан на измерении определенных параметров автомобиля. Например, можно использовать измерение длины оси передней и задней колесной базы, угла поворота передней оси, радиус колес и других параметров. После получения этих данных можно использовать математические формулы для расчета угла поворота.
| Способ | Преимущества | Недостатки |
|---|---|---|
| Специализированное оборудование | — Точные измерения— Мало влияние внешних факторов | — Высокая стоимость оборудования— Сложность установки |
| Математические формулы | — Низкая стоимость— Простота использования | — Возможные погрешности из-за неточности исходных данных |
Выбор способа измерения угла поворота зависит от целей и возможностей пользователя. В случае точных измерений рекомендуется использовать специализированное оборудование, так как оно обеспечивает более точные результаты. Если точность не является приоритетом, то можно воспользоваться математическими формулами.
Практическое применение полученных результатов
Полученные результаты о количестве увеличений модуля перемещения автомобиля при проезде четверти круга могут быть полезны при множестве практических задач. Одной из таких задач может быть определение пройденного расстояния автомобилем при проезде целого круга.
Используя полученное число увеличений модуля перемещения автомобиля при проезде четверти круга, мы можем легко вычислить количество увеличений модуля перемещения при проезде полного круга. Это число будет в два раза больше, чем полученный результат. Таким образом, можно умножить количество увеличений модуля перемещения при проезде четверти круга на два, чтобы найти количество увеличений при проезде полного круга.
Зная количество увеличений модуля перемещения при проезде полного круга, мы можем легко определить полное пройденное расстояние автомобилем. Для этого нужно умножить количество увеличений при проезде полного круга на длину окружности, по которой движется автомобиль. Полученное число будет показывать точное расстояние, пройденное автомобилем.
Таким образом, используя полученные результаты о количестве увеличений модуля перемещения автомобиля, мы можем решать практические задачи, связанные с определением расстояния, пройденного автомобилем при проезде целого круга. Это может быть полезно, например, при планировании пути или определении пройденного расстояния во время тренировок или гонок.
Разбор задачи про четверть круга
В данной задаче нам необходимо определить, сколько раз автомобиль проедет четверть круга при повороте. Для решения этой задачи нам понадобятся некоторые математические знания.
Чтобы определить, сколько раз автомобиль проедет четверть круга, нам нужно знать длину окружности. Длина окружности вычисляется по формуле:
Длина окружности = 2π * радиус
Также нам известно, что четверть круга составляет 90 градусов или π/2 радиан. То есть, мы должны посчитать, сколько раз автомобиль проедет 90 градусов или π/2 радиан, при повороте.
Исходя из этого, наше решение будет следующим:
1. Необходимо найти радиус круга, по которому происходит поворот. Для этого нужно знать длину окружности или диаметр круга.
2. По найденному радиусу вычисляем длину окружности по формуле.
3. Делим длину окружности на длину круга, чтобы определить, сколько раз автомобиль проедет четверть круга при повороте.
Пример решения:
Пусть длина окружности равна 10 метров, а радиус круга равен 2 метра. Тогда:
Длина окружности = 2 * π * радиус = 2 * 3.14 * 2 = 12.56 метров
Количество поворотов = Длина окружности / Длина круга = 12.56 / 10 = 1.256
Таким образом, автомобиль проедет четверть круга примерно 1.256 раза при повороте.



























